Research

My research is primarily in commutative algebra, involving questions inspired by algebraic geometry. In particular, most of my work involves studying Rees algebras/blowup algebras.

I have also begun preliminary projects in mathematical methods for detecting Gerrymandering as well as computational algebraic geometry.

Papers/Preprints

Eddie stands in front of a projector screen at a talk. He points out two specific points on a curve on a slide discussing how to study interesting points.

What are Rees algebras?

The Rees algebra (along with the associated graded ring and the special fiber ring) are known as the “blowup” algebras. They are associated with a process in algebraic geometry called “blowing up.”

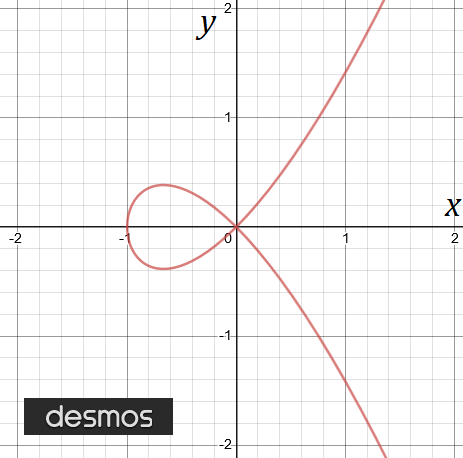
Blowing up can help resolve singularities. Consider the image below. It has a singularity at the origin - where the curve crosses over itself.

There is a curve which crosses over itself at the origin on a 2-dimensional plane.

To “blow up” and remove the singularity, imagine the curve is like a stiff wire that you can “pull apart” in 3-dimensions, giving the following curve which projects onto our original curve.

In a 3-d system, the original curve which intersects itself is displayed on the xy-plane, but there is also a 3-d curve which does not intersect itself, but which would project to the 2-d curve.

The blowup algebras help us figure out the properties of this new curve which doesn’t have singularities.

But the Rees algebra also has applications in pure commutative algebra, geometric modeling, and the study of chemical reaction networks.

It’s definitely worth studying!

There is a blue surface and an orange surface which intersects to give a black curve.

Often, we want to find nonsingular surfaces whose intersection is the blowup. The equations of such surfaces are called the “defining equations” of the blowup, and knowing the defining equations is often key for understanding the blowup in general!

Gerrymandering

The topic of representation in a democracy is challenging. In the United States, states are divided up into districts, and the process of drawing districts is determined by state legislatures. Often, the party in power has an incentive to draw lines to favor their party or disadvantage some group of people. This is referred to as Gerrymandering.

It can be quite challenging to determine when districts are a result of Gerrymandering. Some oddly shaped districts are the result of natural geography or are made to be in compliance with federal law, such as the Voting Rights Act. The district below, Illinois’s 4th Congressional district from 2013-2023, was created to be an opportunity district for Latinx people, in compliance with the Voting Rights Act, so it is not the result of partisan Gerrymandering. Nevertheless, it has a very weird-looking shape and has been referred to as the “earmuffs” district.

A very oddly shaped district on a map of Illinois near Chicago. The district almost resembles a pair of earmuffs.

Additionally, with modern technology, it is possible to Gerrymander with district maps which appear very reasonable-looking. Therefore, it is important to use mathematical modeling to detect Gerrymandering.

In 2013, Jonathan Mattingly and undergraduate student Christy Vaughn applied ensemble analysis to the question of detecting Gerrymandering. In this process, one creates a large number of legally valid district maps. Then a proposed map can be determined to be an outlier or not by comparing it to the ensemble. If the proposed map is an outlier, then there is a reasonable chance it is the result of Gerrymandering. In the past decade, ensemble analysis has been used very widely to study Gerrymandering.

There are many open questions concerning mathematical modeling for detecting Gerrymandering.

To learn more, check out the Metric Geometry and Gerrymandering Group.

A political cartoon with part of Massachusetts. On it is an oddly-shaped district which has been stylized to look like a salamander with a beak and wings.

In 1812, Elbridge Gerry, who was serving as Governor of Massachusetts, signed a district map into law. The map was intentionally designed to benefit the party in power, the Democratic-Republicans. The map had a district which was likened to a salamander, and the above political cartoon was drawn to point out Gerry’s mander.

A screenshot from Zoom containing three people in separate display boxes. Each person is holding up a piece of wood with the same geometric figure present.

Eddie Price (top left), Alessandra Costantini (top right), and Matt Weaver (bottom) holding the blow up of the plane (burned into wood, made by Matt for all of us).

Collaborators

Please check out my collaborators!

This list includes collaborators even for preliminary projects.